CRISTAUX - Cristallochimie minérale

CRISTAUX - Cristallochimie minérale

La cristallochimie est une branche de la chimie s’intéressant à l’étude des corrélations existant entre les compositions chimiques des solides, leur structure et leurs propriétés physico-chimiques. Les lois fondamentales de la chimie s’appliquent à la cristallochimie, auxquelles s’adjoignent quelques autres lois dues à l’état particulier d’organisation des objets chimiques étudiés, les solides. Un exemple: la molécule de méthane (CH⁴) peut être isolée, par dilution dans un gaz inerte; chaque molécule CH⁴ n’interagissant plus avec ses semblables, il est possible d’étudier ses propriétés intrinsèques; par contre, on ne peut isoler une molécule de quartz (SiO²) car l’espèce quartz n’existe qu’en tant que solide, c’est-à-dire en tant que composé organisé possédant la tripériodicité caractéristique de l’état cristallin. La cristallochimie peut donc être définie comme la chimie de l’état solide.

Après quelques brefs rappels sur l’atome et les divers types de liaisons communément admis, on établira les règles de construction des édifices atomiques, et les lois régissant les substitutions au sein de ces édifices. Dans toute la première partie, l’essentiel des exemples sera pris dans des oxydes et silicates; dans la seconde partie, on traitera des composés à liaisons principalement covalentes, les exemples étant choisis essentiellement parmi les sulfures.

1. L’atome et la liaison chimique

Un atome neutre est constitué d’un noyau composé de Z protons et N neutrons autour duquel gravitent Z électrons; Z est le numéro atomique. Chaque électron est caractérisé par quatre nombres quantiques n , l , m ^l , m ^s , appelés respectivement principal (n ), azimutal (l ), magnétique (m ^l ) et de spin (m ^s ). Le principe d’exclusion de Pauli prévoit que deux électrons ne peuvent avoir leurs quatre nombres quantiques identiques. Le nombre quantique n mesure la distance moyenne de l’électron au noyau; c’est lui qui détermine, pour l’essentiel, l’énergie de cet électron: plus les valeurs de n (entier positif) sont élevées, plus l’électron est éloigné du noyau, et plus son énergie est grande. Dans un modèle simple, dit modèle planétaire , on admet que les électrons gravitent autour du noyau, sur des orbites circulaires, chaque orbite étant caractérisée par une valeur différente du nombre n . Dans ce modèle, on assimile l’atome à une sphère; cette approximation est suffisante dans bien des cas. On sera cependant amené à envisager l’atome sous un aspect plus complexe lorsqu’il s’agira d’analyser les effets de champ des ligands; il sera alors nécessaire de tenir compte de la vraie géométrie de l’atome, c’est-à-dire de la répartition fine des densités électroniques autour du noyau. Le modèle planétaire devra céder la place à un modèle purement mathématique, caractérisant le comportement ondulatoire des électrons: la fonction d’onde.

Les cinq grands types de liaisons

Bien que la théorie de la liaison chimique soit maintenant unifiée, il est bon de rappeler les modèles anciens, auxquels il est encore fait référence dans la plupart des cas. Historiquement, ces modèles répondaient à un besoin. On a donc distingué conventionnellement cinq types de liaisons principaux.

– La liaison ionique (ou polaire): dans ce type de liaison, les atomes en contact opèrent un transfert électronique, le plus électronégatif (voir ce concept infra ) attire sur ses proches couches externes les électrons de valence de l’autre atome; chaque atome acquérant la structure du gaz inerte le plus proche. Les atomes ne sont plus neutres mais sont assimilables à des sphères chargées; l’attraction entre ces sphères obéissant à la loi de Coulomb. Exemple: dans le chlorure de sodium (NaCl), il y a transfert d’un électron de Na vers Cl, plus électronégatif que Na. Na⁺ a donc la structure électronique du néon (10 électrons) tandis que Cl^- a acquis celle de l’argon (18 électrons). Ce type de liaison est dominant dans la plupart des sels, oxydes et silicates. La liaison ionique est une liaison non dirigée.

– La liaison covalente (ou homopolaire): lorsque les électronégativités des atomes en présence sont trop peu différentes, le transfert électronique responsable de la liaison ionique ne peut se réaliser. Les atomes en contact mettent alors en commun leurs électrons périphériques, de façon à compléter leurs couches externes. Dans l’exemple du diamant ^{[cf. DIAMANT]}, chaque atome (Z = 6) met en commun ses quatre électrons périphériques avec quatre autres atomes de carbone situés aux quatre sommets d’un tétraèdre régulier entourant l’atome de carbone central.

– La liaison métallique : cette liaison caractérise les atomes métalliques (électropositifs). Le solide métallique peut être considéré comme constitué d’ions positifs baignant dans un «fluide» d’électrons libres. La liberté de ces électrons est responsable des propriétés de conduction électrique et thermique des métaux. Bien que n’étant pas un solide, au sens organoleptique du terme, le mercure présente bien ce type de liaison. Alors que les deux premiers types de liaison décrits sont forts, et du même ordre de grandeur, la liaison métallique est une liaison faible, expliquant les propriétés mécaniques des métaux (malléabilité, ductilité...)

– La liaison de Van der Waals : il s’agit d’une liaison très faible, entre atomes neutres, due à l’existence à chaque instant d’un moment électrique dipolaire non nul, provoqué par le déplacement des électrons autour du noyau. À chaque instant, les centres de gravité du noyau et du nuage électronique ne coïncident pas. Ces liaisons existent par exemple dans les gaz inertes solides, ou dans des minéraux tels que le talc Mg³(Si⁴¹⁰)OH², au sein duquel toutes les couches sont électriquement neutres. Ces couches ne sont liées entre elles que par ces forces de Van der Waals, ce qui confère au talc ses propriétés lubrifiantes. Il en va de même pour la molybdénite (MoS²).

– La liaison hydrogène : l’hydrogène (Z = 1) ne peut apparemment échanger son unique électron qu’avec un seul atome à la fois. Il est fréquent de constater que cet atome d’hydrogène interagit avec plusieurs atomes. Bien que la petite taille de l’atome d’hydrogène ne lui permette pas de s’entourer de plus de deux atomes, on connaît des cas d’interaction par liaison hydrogène entre un dipôle OH et trois, quatre, six voisins oxygène (phyllosilicates, inosilicates, cyclosilicates). L’énergie de la liaison hydrogène est environ cent fois plus faible que celle de la liaison ionique. Cette liaison hydrogène assure la stabilité de composés tels que les sels hydratés, par exemple: la chalcanhite (CuSO⁴,5H²O).

Les cinq types de liaison qui viennent d’être décrits sont unifiés dans la résolution de l’équation de Schrödinger, qui donne la densité électronique en tout point de la molécule (donc du solide).

L’énergie réticulaire

«L’énergie réticulaire d’un cristal ionique est l’énergie nécessaire pour disperser, en ions séparés, une masse de ce cristal correspondant à une mole» ^{[cf. MINÉRALOGIE]}.

La contribution principale à l’énergie de liaison des cristaux ioniques est électrostatique; on l’appelle énergie de Madelung . Dans un cristal ionique, deux autres types d’énergie d’interaction existent: les interactions répulsives entre nuages électroniques et entre noyaux et les attractions de type Van der Waals. L’ordre de grandeur de ces deux derniers types d’énergie les rend négligeables devant la seule énergie d’attraction électrostatique. On montre que l’énergie réticulaire d’un cristal composé de deux types d’atomes (par exemple NaCl), contenant 2N ions distants de R ⁰ à l’équilibre s’écrit:

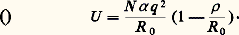où q est la charge d’un ion, 福 un paramètre empirique caractérisant la répulsion, ayant la dimension d’une distance et 見 une constante, dite constante de Madelung, dont la valeur approchée est 1,75.

Dans l’équation (1), tous les termes à droite sont connus, excepté 福 . Ce paramètre est déductible de la mesure du module de rigidité B :

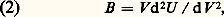où V est le volume occupé par les 2N ions. Les mesures expérimentales de ce module de rigidité permettent l’évaluation de 福 et montrent que la répulsion s’exerce à une distance 福 de l’ordre de 0,03 nanomètre (nm).

Propriétés géométriques des ions, influence de l’environnement

Les rayons ionique et atomique

Les notions de rayons ionique et atomique sont fécondes, mais reposent sur une approximation. Elles ne prennent de sens que si l’on admet la sphéricité parfaite des ions et des atomes, ce qui est rarement réalisé (on peut considérer comme sphériques les ions alcalins tels que Rb⁺ et Cs⁺, ou les ions halogènes tels que C1^-, Br ^-, I^-); par contre, des ions d’éléments de transition, tels que Fe²⁺ ou Mn³⁺, n’auront jamais la symétrie sphérique. On peut cependant attribuer à chaque atome un rayon, qui est une mesure de son encombrement. Faute de pouvoir délimiter avec précision l’étendue des nuages électroniques, on mesure les rayons atomiques et ioniques par une méthode indirecte. La radiocristallographie permet des mesures d’une extrême précision des distances entre centres d’atomes. Si deux atomes identiques sont en contact, on définira leur rayon comme la demi-distance entre leurs centres. Par exemple, dans le quartz, chaque atome de silicium est au centre d’un tétraèdre dont chacun des quatre sommets est occupé par un atome d’oxygène. Les atomes d’oxygène sont en contact le long des côtés du tétraèdre; on définira le rayon ionique de l’oxygène, dans ce cas, comme la demi-distance entre les centres de deux oxygènes adjacents. La distance entre deux atomes d’oxygène dans le quartz est égale à 0,27 nm, ce qui donne 0,135 nm pour le rayon ionique de l’oxygène. Si les atomes (ou ions) ne sont pas identiques, on ne pourra connaître le rayon atomique (ou ionique) de l’un qu’en connaissant le rayon de l’autre. Reprenons l’exemple du quartz, le rayon ionique du silicium, au centre du tétraèdre de quatre oxygènes est calculable selon la relation r ^Si = d ^Si-O 漣r ⁰, où r ⁰ est le rayon ionique de l’oxygène, précédemment mesuré. La distance d ^Si-O, mesurée par diffraction des rayons X est 0,161 nm, d’où l’on calcule le rayon ionique du silicium dans le quartz: r ^Si = 0,161 漣 0,135 = 0,026 nm.

Du fait de la définition du rayon atomique (ou du rayon ionique), qui n’est que la différence entre deux longueurs, on peut aboutir à des «rayons négatifs», lorsque la distance entre les centres des atomes liés est inférieure au rayon de l’un de ces atomes. Les cas de ce type sont rares, on les rencontre dans des composés à liaison semi-covalente, tels que les groupements OH ou CH. On admet pour «rayons ioniques» de H et C, respectivement 0,038 nm (H dans un groupement OH) et 0,008 nm (C dans un groupement CH³). Ces valeurs négatives ne sont que des conséquences de la définition des rayons.

Une autre conséquence fondamentale de la définition est la variabilité du rayon, ionique par exemple, avec le nombre d’ions voisins, de signe opposé, auxquels l’ion central est lié. Prenons le cas de l’aluminium, le rayon ionique de Al³⁺ est de 0,039 nm lorsque l’aluminium est lié à quatre atomes d’oxygène, constituant un tétraèdre; il est de 0,053 nm lorsque ce même ion Al³⁺ est lié à six atomes d’oxygène constituant un octaèdre. Cette différence est due au fait que Al³⁺ n’a pas le même encombrement dans les deux types de polyèdres. Pour la même raison, un élément à valence variable, dont le nombre d’électrons périphériques n’est donc pas constant, possédera autant de valeurs du rayon ionique que d’états de valence, pour un environnement donné. Par exemple, le vanadium, dans un site octaédrique oxygéné aura pour rayons ioniques: V²⁺ : 0,079 nm; V³⁺ : 0,064 nm; V⁴⁺ : 0,059 nm; V⁵⁺ : 0,034 nm. On observe clairement, sur cet exemple, que plus l’état de valence est élevé, pour ces cations, dû aux départs successifs de plusieurs électrons, plus le rayon ionique est petit, c’est-à-dire, plus l’encombrement du nuage électronique restant est faible.

L’électronégativité et la polarisation

L’électronégativité est la propriété qu’a un atome d’attirer une partie du nuage électronique de l’autre. Dans le couple d’atomes A-B, il y a renforcement de l’énergie de liaison par ce déplacement électronique. Pauling a établi une loi empirique donnant cette énergie de liaison supplémentaire: E 力100(x ^A 漣 x ^B)², où x ^A et x ^B sont les électronégativités des deux atomes A et B. Dans le tableau périodique des éléments, les électronégativités croissent de bas en haut dans chaque colonne (de Cs à Li pour les éléments alcalins, de I à F pour les halogènes); et de gauche à droite; l’élément le plus électronégatif étant le fluor. La notion d’électronégativité aboutit au concept de charge partielle, puisque, du fait du transfert électronique d’un atome vers l’autre, la densité électronique croît au voisinage de l’un et décroît au voisinage de l’autre; on décrira alors les deux atomes comme possédant l’un une charge partielle positive, l’autre une charge partielle négative. La polarisation est cette déformation du nuage électronique d’un atome, soumis au champ électrique d’un atome voisin. Ce phénomène est fréquent dans le cas des gros anions, dont les électrons périphériques subissent peu l’influence du noyau central et sont donc aisément attirables par des petits cations fortement chargés. Ce phénomène tend à diriger la liaison ionique et à lui donner un caractère de plus en plus covalent, au fur et à mesure que, à charge égale, la dimension du cation central diminue dans un polyèdre (cf. structures IONIQUES).

2. Principes fondamentaux de la construction des édifices cristallins

La coordinence. Première loi de Pauling

Autour de chaque cation, un polyèdre anionique se constitue, en donnant un assemblage aussi compact que possible. Le rapport des rayons cationique (r ^C) et anionique (r ^A) régit le nombre d’anions pouvant jouxter le cation central. Ce nombre d’anions est la coordinence (ou nombre de coordination) du cation central (tabl. 1).

Certains éléments chimiques, ayant une taille compatible avec plusieurs types de polyèdres de coordination, avec le même anion, pourront se rencontrer sous des coordinences diverses (par exemple Zn peut exister en coordinence IV ou VI, Al en coordinences IV, V et VI, Na en coordinences VI ou VIII, avec l’oxygène).

L’équilibre des valences électrostatiques. Deuxième loi de Pauling

La deuxième loi de Pauling s’énonce ainsi: la somme des valences électrostatiques reçues par un anion, de la part des cations qui lui sont liés, est égale à la valence de cet anion (cette règle est symétrique et s’applique de la même façon en considérant le cation). La valence électrostatique, ou valence échangée dans la liaison, est définie comme le rapport «charge sur coordinence», si le polyèdre de coordination est régulier. S’il est irrégulier, différents modèles mathématiques permettent de calculer ces valences de liaison, pour chaque liaison, en fonction de la distance cation-anion. Ces modèles sont de la forme v = vⁱ (d /d ⁰)^-4 où vⁱ est la valence électrostatique théorique dans le cas d’un polyèdre régulier, définie ci-dessus comme le simple rapport charge/coordinence, d ⁰ est la distance cation-anion dans le polyèdre régulier (les valeurs de d ⁰ sont tabulées pour la plupart des couples cation-anion), d est la distance cation-anion réelle dans le polyèdre irrégulier. Cette règle signifie que, pour qu’un édifice cristallin ionique soit stable, il ne suffit pas que la neutralité électrique soit réalisée globalement, mais que celle-ci doit l’être dans chacun des polyèdres de coordination.

Troisième, quatrième et cinquième lois de Pauling

La troisième loi de Pauling prévoit que l’existence d’arêtes, et plus encore de faces, communes à deux édifices anioniques, affaiblit la stabilité de la structure, et ce d’autant plus que le cation central est chargé, en coordinence faible et de taille proche de la limite permise par les dimensions du polyèdre anionique. Cela revient, pour toute structure, à éloigner au maximum les uns des autres les cations fortement chargés. Dans les silicates, les tétraèdres Si⁴ seront soit isolés, séparés par des polyèdres dont le cation central est à basse charge (comme dans les mésosilicates: olivines, grenats), soit liés par la mise en commun d’un oxygène et d’un seul par tétraèdre (comme dans les tectosilicates: quartz). Ces tétraèdres ne s’accolent pas par une arête commune, ni par une face.

La quatrième loi de Pauling indique que dans une structure, lorsque plusieurs types de polyèdres sont présents, ceux dont le cation central est de charge élevée s’éloignent au maximum les uns des autres. Cette quatrième règle peut être incluse dans la troisième, dont elle n’est que la conséquence logique.

La cinquième loi de Pauling stipule que, dans une structure cristalline, le nombre de types de polyèdres présents est faible. Cela découle de la tendance à la formation, par les atomes, d’empilements aussi compacts que possible.

La diadochie

Les règles de diadochie précisent les conditions dans lesquelles les ions peuvent se substituer l’un à l’autre dans une structure cristalline. Ces lois découlent de l’observation et ont été énoncées, pour la plupart, il y a plusieurs décennies; elles sont connues sous le nom de lois de Goldschmidt ; on en présente ici une actualisation:

– deux ions ayant des propriétés chimiques voisines ne se remplaceront aisément que si leurs rayons diffèrent de moins de 15 p. 100 (exemples: remplacement de Mg (0,072 nm) par Ni²⁺ (0,070 nm) ou par Fe²⁺ (0,077 nm); impossibilité du remplacement de Na⁺ (0,098 nm) par K⁺ (0,133 nm), sauf à très haute température);

– lorsque deux ions chimiquement voisins sont en compétition pour leur fixation dans un site cristallin, celui qui sera incorporé préférentiellement est celui qui entraînera le moins de perturbation dans la structure, c’est-à-dire celui dont le rayon ionique est aussi proche que possible de la dimension du site d’accueil. Ce n’est pas nécessairement le plus petit des deux (exemples: Cs (0,167 nm) est incorporé plus facilement que K (0,133 nm) dans le réseau de la leucite);

– le remplacement d’un ion par un autre, de charge différente, ne sera possible que si une seconde substitution rétablit l’équilibre global des charges (neutralité électrique) ainsi que les équilibres locaux , dans chacun des polyèdres (cf. Deuxième règle de Pauling). On parle dans ce cas de substitutions couplées. Exemple: Na⁺ + Si⁴⁺ remplacés par Ca²⁺ + Al³⁺ dans les feldspaths plagioclases;

– règle de Ringwood (1955): lorsque deux ions de même taille sont en compétition pour un même polyèdre anionique, c’est celui qui a la plus petite électronégativité qui est incorporé préférentiellement. Exemple: pas de remplacement possible entre Na⁺ (0,098 nm; électronégativité 118 calories) et Cu⁺ (0,096 nm; électronégativité 177 calories) dans les oxydes;

– enfin, certains complexes anioniques ne peuvent pas se remplacer, soit parce qu’ils n’ont pas la même configuration (exemple SiO^44- et B^32-) ou pas la même charge cationique, bien que leur configuration soit semblable (exemple SiO^44- et V^43-), soit, enfin, en raison de tailles trop différentes (exemple SiO^44- et Sn^44-).

En ce qui concerne les remplacements d’éléments en traces, de propriétés voisines, tels que les alcalins entre eux, ou les alcalino-terreux entre eux, voire les halogènes entre eux, on a établi récemment une loi simple, qui indique que la plus ou moins grande facilité de ces remplacements, mesurable par l’énergie mise en jeu pour les réaliser, est fonction d’un paramètre structural d’adaptation de l’ion à son site, qui mesure, dans le cas des remplacements cationiques, la déformation du réseau anionique qu’ils provoquent.

3. Comparaison des structures

L’isomorphisme

Au sens ancien du terme, l’isomorphisme cristallin de deux solides caractérise l’existence simultanée de trois propriétés: ces solides sont homéomorphes, c’est-à-dire que leurs réseaux appartiennent au même groupe spatial; les substances qui les constituent sont aptes à la syncristallisation qui entraîne l’existence de cristaux mixtes; enfin, la constitution chimique de ces substances doit être voisine. Cette troisième condition est corollaire de la deuxième. Pour que deux substances puissent être isomorphes, il faudra donc qu’elles présentent des analogies chimiques (par exemple: chlorures et bromures des mêmes éléments), qu’elles possèdent des ions de même valence (par exemple: Mg²⁺, Fe²⁺, Ni²⁺, Mn²⁺ dans les ilménites, les pérovskites, les spinelles...) et dont les dimensions soient voisines. Cela découle des règles de diadochie.

L’isotypisme

Des substances peuvent être structuralement équivalentes sans qu’il soit possible de parler d’isomorphisme, du fait de leur inaptitude à former des cristaux mixtes. C’est par exemple le cas du chlorure de sodium (NaCl), de l’oxyde de magnésium (MgO) et du sulfure de calcium (CaS) dans lesquels les positions cationiques (Na, Mg, Ca) sont les mêmes, de même que les positions anioniques (Cl, O, S), sans qu’existe aucun cristal mixte entre ces espèces. On a créé le terme d’anti-isotypisme pour désigner des solides ayant le même type de réseau cristallin, mais dans lesquels les positions cationiques de l’un sont les positions anioniques de l’autre. Par exemple, les oxydes alcalins (Na²O, K²O) et la fluorine (CaF²) sont anti-isotypiques.

Le polymorphisme

Il y a polymorphisme lorsqu’un solide peut se présenter sous plusieurs formes cristallines différentes, ayant donc des propriétés physiques différentes, bien que de même composition chimique. C’est par exemple le cas du carbone (graphite, diamant), du quartz (formes 見 et 廓), de ZnS (blende ou wurtzite, voir la deuxième partie de l’article). Le passage d’une forme à l’autre est une transformation polymorphique (exemple: la forme graphite du carbone donne la forme diamant du même carbone, à haute température – de l’ordre de 1 500 ⁰C – et haute pression – de l’ordre de 5 000 mégapascals. Ces transformations ont donc lieu sous l’effet de la température et de la pression, comme dans le cas du carbone, ou sous l’effet de la seule température, comme dans le cas du fer métallique pur qui a un réseau cubique centré au-dessous de 900 ⁰C, cubique à faces centrées entre 900 et 1 400 ⁰C, et à nouveau cubique centré de 1 400 ⁰C au point de fusion.

Le polytypisme

Le polytypisme est un cas particulier du polymorphisme. Les polytypes diffèrent par la manière dont sont empilées des couches identiques dans la structure. Les dimensions de ces couches élémentaires sont identiques, dans leur plan; seule l’épaisseur diffère, une «couche épaisse» n’étant qu’un multiple de la couche élémentaire. D’un polytype à l’autre, pour une même substance, les environnements locaux sont peu variables, bien que le système cristallin puisse être différent. On connaît particulièrement bien le polytypisme de SiC (carborundum) et des phyllosilicates (argiles, micas).

Les structures types

Par commodité, il a été défini un certain nombre de structures de référence, dont bon nombre de composés (corps purs, composés binaires ou ternaires) sont isotypes. Ainsi, on parlera de structure «type NaCl» (réseau cubique à faces centrées, chaque ion Na⁺ étant au centre d’un octaèdre Cl^-, de même que chaque ion Cl^- est au centre d’un octaèdre Na⁺). Ce type structural, imposé par le rapport r ^A/r ^C principalement (0,41 à 0,73), se rencontre dans les composés très divers, tels que: les halogénures LiF, LiCl, LiBr, LiI, NaF, NaCl, NaBr, NaI, KF, KCl, KBr, KI, RbF, RbCl, RbBr, RbI, AgCl, AgBr; les oxydes MgO (périclase), CaO, SiO, BaO, VO, MnO, FeO, CoO et NiO; les sulfures MgS, CaS, SrS, BaS, MnS, PbS (galène).

Pour des rapports r ^A/r ^C inférieurs à 0,41, le cation, au centre du polyèdre anionique, ne pourra plus s’entourer de six voisins (octaèdres), mais se trouvera dans la coordinance immédiatement supérieure (cube); cela entraîne la formation d’un autre type de structure, le type CsCl (réseau cubique centré, chaque Cs⁺ étant au centre d’un cube de huit Cl^-). Des halogénures tels que CsBr, CsI, NH⁴Cl appartiennent à ce type.

On reconnaît de même des structures de type diamant (carbone, silicium, germanium); de type sphalérite (blende), pour CuCl, CuBr, CuI, ZnS, ZnSe, ZnTe, CdS, CdSe, AlP, GaP, GaAs, etc; de type wurtzite (formule chimique ZnS, tout comme la blende), adoptée par BeO (oxyde de béryllium), ZnO (zincite), CdS (greenockite), des nitrures tels que AlN, GaN, InN...

4. Théories particulières

Théorie du champ cristallin

La théorie du champ cristallin est une théorie électrostatique de la liaison chimique entre cations de métaux de transition et anions (les ligands), considérés comme charges ponctuelles. Cette théorie n’est applicable qu’aux réseaux dans lesquels la liaison chimique peut être considérée comme principalement ionique, et aux ions n’ayant que des remplissages partiels de leurs orbitales externes: orbitales 3 d pour les éléments de transition de la première série, du scandium au zinc, orbitales 4 d pour la deuxième série, de l’yttrium au cadmium, et orbitales 5 d pour la troisième série, du hafnium au mercure, plus le lanthane; enfin, orbitales 4 f pour les terres rares.

Rappels sur la structure des orbitales d

Les orbitales s ont la symétrie sphérique et sont centrées sur le noyau de l’atome. Les orbitales p, au nombre de trois, sont identiques, constituées chacune de deux lobes de signe opposé et dirigées selon chacun des trois axes x, y et z d’un repère orthonormé, dont l’origine est le noyau atomique. Par contre, les orbitales d, au nombre de cinq, se divisent en deux groupes bien distincts: trois orbitales diagonales, dont les lobes «pointent» entre les axes de coordonnées; orbitale d^xy entre les axes x et y , orbitale d^yz entre les axes y et z , et orbitale d^xz entre les axes x et z ; le second groupe est constitué de deux orbitales axiales, dont les lobes «pointent» sur les axes de référence, l’une est l’orbitale d^{x 2} size=1^{漣y 2} aux lobes dirigés selon les axes x et y , l’autre est l’orbitale d^{z 2} aux lobes dirigés selon l’axe z .

Dans un ion d’élément de transition libre, les cinq orbitales d ont le même niveau d’énergie (état dégénéré) et ont donc toutes la même probabilité d’occupation par les électrons. Si l’ion de métal de transition est incorporé à une structure cristalline, la non-sphéricité du champ électrostatique autour de l’ion, imposée par la structure, provoque une levée de la dégénérescence des niveaux d’énergie des orbitales d , certaines se trouvant dans un état énergétique inférieur, d’autres dans un état énergétique supérieur à l’état énergétique dégénéré de l’ion libre. Il y a donc «éclatement» des niveaux énergétiques de ces orbitales, par rapport au centre de gravité des niveaux énergétiques. La nature et l’importance de cet «éclatement» dépendent du type de ligand et de la symétrie de la répartition de ces ligands autour de l’ion central. Les orbitales d n’ayant plus toutes le même niveau d’énergie, leur remplissage par les électrons ne se fera plus de façon aléatoire, ceux-ci peuplant de préférence, et comme le prévoit la thermodynamique, les niveaux d’énergie les plus bas, c’est-à-dire les orbitales les plus éloignées des ligands; en d’autres termes, les électrons, charges négatives de l’ion central, s’éloignent au maximum des ligands, chargés négativement eux aussi.

Tout électron peuplant une orbitale de basse énergie stabilisera l’ion dans le champ cristallin, tout électron peuplant une orbitale de haute énergie produira l’effet inverse. Le bilan énergétique de cette répartition électronique entre les orbitales de différents niveaux est la C.F.S.E., abréviation de Crystal Field Stabilization Energy.

Exemple d’un champ octaédrique

Dans un octaèdre, défini par six ligands, ceux-ci sont situés sur les trois axes x , y et z , à proximité donc des lobes des deux orbitales axiales d ^{x 2} size=1^{漣y 2} et d ^{z 2}. Il y a éclatement en deux groupes des cinq orbitales d ; un premier groupe, constitué par les trois orbitales diagonales (d ^xy , d ^yz et d ^xz ), qui sont les orbitales les plus éloignées des ligands et donc de basse énergie, et un second groupe, constitué par les orbitales axiales proches des ligands et donc de haute énergie. Ce sont les orbitales diagonales, donc les orbitales de basse énergie, qui sont peuplées les premières lors du remplissage des orbitales d par les électrons. L’énergie séparant ces deux niveaux est désignée par ^o dans l’octaèdre (cette différence est désignée par ^t dans les tétraèdres, par ^c pour les champs cubiques, etc.). Tout électron occupant une orbitale de basse énergie stabilise l’ion dans ce site octaédrique, d’une fraction de ^o (2/5 ^o exactement); tout électron occupant une orbitale de haute énergie déstabilisera ce même ion dans ce site, d’une autre fraction de ^o (3/5 ^o exactement). L’ion Ti³⁺, par exemple, qui ne possède qu’un unique électron d , acquiert une énergie de stabilisation de 2/5 ^o, dans un champ octaédrique.

^o est fonction du type de ligand ( est grand dans les cyanures, moyen dans les oxydes et faible dans les halogénures), de la charge portée par ces ligands, et de la distance entre les ligands et l’ion central.

Conséquences

, qui est une énergie, est de l’ordre de quelques dizaines de kilocalories par mole. Cette énergie est proche de l’énergie quantique h 益 des photons du spectre visible. Les photons dont l’énergie sera exactement égale à seront donc absorbés par l’ion, créant des transitions électroniques et entraînant le peuplement des niveaux d’énergie élevée. Cela est à l’origine de la plupart des phénomènes de coloration rencontrés dans les solides, et en particulier dans les minéraux: Cr³⁺ dans le rubis, Ti³⁺ dans le saphir, Fe³⁺ dans l’améthyste, Fe²⁺ dans les grenats, Cu²⁺ dans le dioptase, etc.

La théorie du champ cristallin permet de prévoir les distributions intrasites des ions d’éléments de transition au sein d’un composé, ainsi que leur répartition entre phases différentes cristallisant en même temps. Si plusieurs types de sites cristallins coexistent dans une même phase, il existe une valeur de pour chacun de ces sites; on montre qu’il existe une relation entre ces valeurs qui sont dans le rapport ^o : ^c : ^t = 1 : 8/9 : 4/9. La répartition des ions entre les différents sites, possédant des énergies de stabilisation différentes, obéit à une loi de type Maxwell-Boltzmann:

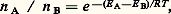où n ^A et n ^B sont les nombres d’ions peuplant les deux sites A et B, d’énergie E ^A et E ^B, R est égal au produit de face=F9796 , nombre d’Avogadro, par k , la constante de Boltzmann, et T , la température absolue.

Lorsque les liaisons chimiques ne sont pas de type ionique, mais de type covalent, la théorie du champ cristallin est inapplicable car les orbitales de l’ion central et des ligands se recouvrent, les ligands ne peuvent plus être considérés comme des charges ponctuelles. Il est nécessaire d’introduire une nouvelle théorie, celle des orbitales moléculaires, applicable aux composés covalents, et en particulier au groupe minéralogique des sulfures et composés voisins.

Théorie des orbitales moléculaires: modèle de liaison covalente ; introduction à la cristallochimie des sulfures

Les sulfures représentent le principal groupe minéralogique ayant des liaisons chimiques covalentes, parmi les matériaux terrestres accessibles à l’homme. Les besoins en métaux de l’humanité ont, dès le début de son activité minière, été largement satisfaits par des sulfures. Un nombre croissant de sulfures et autres composés, structuralement semblables, sont utilisés dans l’industrie, du fait de leurs propriétés physiques particulières. Notre compréhension de la cristallochimie de ces composés a souvent été contrariée par la complexité des problèmes posés. Deux modèles sont nécessaires à la description de la liaison dans les sulfures et autres substances cristallines de même type. Bien que les exemples soient pris, ci-après, dans les sulfures, ces modèles sont d’application générale.

Lorsque les recouvrements d’orbitales des ligands et du métal sont importants, les simplifications contenues dans le modèle du champ cristallin sont excessives; ces situations doivent être traitées par la théorie des orbitales moléculaires. Lorsque des atomes s’assemblent en molécules (ou en édifices plus complexes), leurs orbitales atomiques, qui se recouvrent, se combinent en orbitales moléculaires. Chaque combinaison d’une orbitale cationique et d’une orbitale anionique donne une orbitale liante , dont l’énergie est inférieure à celles des deux orbitales originelles, et une orbitale antiliante , dont l’énergie est supérieure à celle de ces orbitales originelles. Le recouvrement des orbitales atomiques dépend des propriétés de symétrie des orbitales du métal et des ligands, et de la forme du polyèdre de configuration.

Par exemple, considérons un métal de transition dans un site octaédrique régulier, entouré de six ligands (la proportion des éléments de transition dans le globe terrestre, 40 p. 100 en poids, justifie le choix d’un tel exemple). Trois des cinq orbitales d pointent vers les ligands, et se combinent avec une orbitale s et trois orbitales p, donnant six orbitales hybrides d² s p³. Celles-ci sont toujours dirigées vers les ligands et se recouvrent avec les orbitales s et p de ces ligands, donnant naissance à des orbitales liantes et antiliantes. Les orbitales liantes sont totalement occupées par des électrons appariés, tandis que les électrons excédentaires vont peupler les orbitales antiliantes, à plus haute énergie. Les trois autres orbitales d pointent entre les ligands et ne participent pas à la liaison 靖 (c’est-à-dire à un recouvrement orbital direct). Ces orbitales non liantes peuvent cependant participer à un recouvrement indirect avec d’autres orbitales d des ligands, baptisé liaison 神.

De même que dans le cas du champ de ligands, le cation d’un métal de transition ayant de quatre à sept électrons d peut se trouver dans deux états, qui diffèrent par la répartition des électrons entre les orbitales d: l’état haut spin , lorsque le maximum possible d’électrons ne sont pas appariés, et l’état bas spin , lorsque la différence d’énergie entre orbitales antiliantes et non liantes dans le champ de ligands octaédrique contraint les électrons à s’apparier dans les orbitales de plus basse énergie. Dans les sulfures, seuls Co et Ni sont stabilisés dans des états à bas spin, tandis que dans les disulfures (sulfures contenant des groupements S^22-), on rencontre également dans l’état bas spin Fe (en site octaédrique).

L’état de spin des métaux exerce une influence majeure sur les distances interatomiques, de même que sur les propriétés électriques et magnétiques de ces composés.

Théorie des bandes d’énergie

Malgré le succès de la théorie des orbitales moléculaires pour l’explication des liaisons dans les sulfures, leur caractère métallique, souvent même leur conductivité métallique et leur paramagnétisme de Pauli suggèrent que tous les électrons de valence ne soient pas localisés sur les sites cationiques. Pour cette raison, depuis des années, la théorie des bandes dans les solides cristallins a été employée intensivement pour expliquer la liaison et les propriétés physiques des sulfures.

Avec un recouvrement important des orbitales électroniques, et conformément au principe d’exclusion de Pauli (qui ne permet pas à plus de deux électrons d’être dans le même état énergétique au sein d’un même groupement), les énergies, pour chaque orbitale, seront confinées à un certain domaine. Plus le recouvrement est intense, plus la largeur de la bande d’énergie est grande. Ainsi, les orbitales liantes formeront une bande de valence , pleine, tandis que les orbitales antiliantes (partiellement occupées ou totalement vides) représenteront une bande de conduction . Les bandes dues aux électrons d sont généralement situées entre ces deux types, et les propriétés des composés ne dépendront pas uniquement de l’écart entre les bandes principales, de valence et de conduction (cf. physique des SOLIDES), mais aussi de la bande d par rapport à elles (intermédiaire – proche – en recouvrement) et du taux de remplissage de cette bande. Rarement, les orbitales d se recouvrent (liaison métallique) et forment aussi des bandes d’énergie larges.

5. Caractères des liaisons spécifiques aux sulfures

Pour la plupart des éléments, les structures des sulfures diffèrent considérablement de celles des oxydes correspondants, mais sont d’habitude semblables à celles des séléniures correspondants. On présente ci-après les raisons principales de ces différences: le soufre et le sélénium sont beaucoup moins électronégatifs que l’oxygène, de sorte que la covalence est de bien plus grande importance dans les sulfures et séléniures métalliques que dans les oxydes. Une autre conséquence est que S^2- et S^e2- sont fréquemment oxydés, sous les valences effectives S^- et Se^-, par certains ions métalliques, et forment souvent des paires covalentes S^22- et Se^22-. Les ions sulfure et séléniure sont plus gros que les ions de type oxyde et ont aussi une bien plus grande «polarisabilité». Pour cette raison, S^2- et Se^2- ont fréquemment un environnement polarisé, asymétrique dans la structure (alors que les ions O^2-, dans les oxydes, ne sont généralement pas polaires). Pour cette raison, les structures feuilletées sont communes dans les sulfures et les séléniures. Enfin, les ions sulfure et séléniure ont des niveaux d’énergie des orbitales d assez bas pour participer à la liaison avec des métaux, la coordinence de l’anion étant alors différente (le plus souvent supérieure), de ce qu’elle est dans le cas de l’oxygène.

Les facteurs principaux qui gouvernent la stéréochimie des sulfures sont la charge et la configuration électronique des cations (dans l’état fondamental ou dans un état excité). Les polyèdres de coordination des métaux, les plus fréquents dans les sulfures, sont des tétraèdres ou octaèdres réguliers ou distordus; plus rarement, on rencontre le métal dans une coordinence plane carrée (Pt²⁺, Pd²⁺), plane triangulaire (Cu⁺, Ag⁺), linéaire (Hg⁺, Ag⁺, Cu⁺) ou prismatique trigonale (Mo⁴⁺, W⁴⁺, Nb⁵⁺, Ti⁵⁺, Pb²⁺). Zn²⁺, Ca²⁺, Ga³⁺, Ge⁴⁺, As⁵⁺ et Sb⁵⁺ sont pratiquement toujours en coordinence tétraédrique avec le soufre, ainsi que, parfois, In³⁺, Sn⁴⁺, Cu, Fe, Mn, Co (ces trois derniers métaux de transition ont une grande solubilité dans ZnS) et Ni.

Les distorsions dues à l’effet Jahn-Teller sont rares dans les sulfures de métaux de transition, du fait de la délocalisation des électrons.

6. Types de structures et de familles dans les sulfures

Du fait de l’hybridation tétraédrique ou octaédrique des orbitales de l’atome métallique, bon nombre de structures de sulfures peuvent être décrites comme un empilement compact (ou presque compact) d’atomes de soufre ménageant des sites octaédriques et/ou tétraédriques occupés par les atomes métalliques. Tout en ménageant des sites de multiplicité appropriée et des longueurs de liaisons adéquates pour les cations, un tel arrangement éloigne autant que nécessaire les plus proches voisins (ions de même charge). Ainsi, les grandes familles structurales, dont les types sont la sphalérite ( 廓-ZnS), la galène (PbS), les thiospinelles (tels que FeNi²S⁴), et la pyrite (FeS², avec les groupements S^22- pris comme unité structurale), peuvent être considérées comme dérivant de l’empilement cubique compact; les structures de type wurtzite ( 見-ZnS), nickéline (NiAs, ou pyrrhotite Fe^1-x S, par exemple), et, dans une large mesure, molybdénite (MoS²) et marcassite (FeS²) sont des approximations de l’empilement hexagonal compact (tabl. 2, fig. 1 et 2). Chaque famille donne des dérivés substitués , avec deux types de cations (ou d’anions) remplaçant (d’une manière ordonnée, au moins à basse température) le constituant simple du départ, des dérivés lacunaires , ayant une partie des sites (cationiques habituellement), vacants, des dérivés géométriquement distordus ou, enfin, des dérivés dans lesquels certaines positions initialement vacantes sont occupées (tabl. 2). Les sulfures et séléniures de Ag et Cu ont des structures très complexes, toujours fondées sur l’empilement compact des atomes S ou Se.

À des températures modérément élevées, comprises entre 60 ⁰C et 200 ⁰C, les structures complexes des sulfures de Cu et Ag (et de quelques sulfures ternaires contenant ces métaux), dont les atomes Ag et Cu sont fixes, se transforment en phases de haute température dans lesquelles Cu⁺ et Ag⁺ se distribuent sur tous les sites disponibles et deviennent extrêmement mobiles le long des chenaux du réseau anionique, conférant au cristal une conductivité ionique élevée à l’état solide.

Les liaisons métal-métal , qui existent lorsque les distances inter-métalliques MeMe sont proches de celles que l’on rencontre dans les métaux purs, jouent un grand rôle dans la cristallochimie de certains sulfures métalliques. Ces composés montrent souvent des compositions étranges par rapport aux règles traditionnelles de la valence, comme, par exemple, la famille de la pentlandite (Fe, Ni, Co)⁹S⁸ qui contient des groupements cubiques de huit tétraèdres de coordination (Fe, Ni, Co) liés par leurs arêtes, et ayant trois liaisons Me-Me par atome métallique, tout comme certains sulfures: Ni³S², 見-Ni⁷S⁶ et In⁶S⁷. Cependant, bon nombre de sulfures ayant une composition «classique» ont aussi des liaisons Me-Me: la nickéline (NiAs, fig. 2), la mackinawite (FeS), la cubanite (CuFe²S³), diverses phases sulfurées Cu^2-x S, KCu⁴S³, Ag²S, InS, GaS. L’existence de liaisons Me-Me (et des groupements métalliques qu’elles induisent) est particulièrement fréquente dans les composés d’éléments 4 d, 5 d, 4 f, avec divers anions.

Les cations ayant la configuration s ² (une paire d’électrons non liés) ont généralement des environnements polarisés. Leur coordinence peut être interprétée en terme d’hybridation sp, ou spd, avec l’une des orbitales hybrides occupée par les deux électrons non engagés dans la couche de valence; elle est essentiellement non liante. Les autres orbitales hybrides se combinent avec les orbitales anioniques remplies, conduisant à des coordinations de type pyramide trigonale [MeS³] pour As³⁺, Sb³⁺, Ge²⁺, Sn²⁺ et Te⁴⁺ ou du type pyramide à base carrée [MeS⁵], typique de beaucoup de structures contenant Sb³⁺ et de la majorité de celles qui contiennent Bi³⁺. Comme les propriétés métalliques de ces éléments croissent avec leur numéro atomique, la différence d’énergie entre les orbitales s et p s’accroît et conduit à une diminution du taux d’hybridation sp. Ainsi, considérablement moins polarisés ou même non polarisés sont les environnements de Tl⁺, Pb²⁺, et aussi Bi³⁺.

Les paires d’électrons non engagées s’arrangent habituellement en domaines étendus, comme le font les parties semi-octaédriques des polyèdres de coordination de ces cations, conduisant à des structures composées de feuillets, îlots ou blocs d’éléments de type galène, séparés par des interstices dont la coordination est irrégulière. Cette situation est particulièrement typique des sulfures complexes de Pb, Ag, Fe, Tl, Cu (Mn-Hg), avec As, Sb ou Bi, dénommés sulfosels de ces métaux. Les grands prismes trigonaux et octaèdres de coordination sont primordiaux dans ces structures, spécialement pour ce qui concerne la création d’interstices irréguliers. Les structures de sulfures de lanthanides, très semblables et tout aussi complexes, sont elles aussi fondées sur la combinaison de polyèdres de coordination des cations constituants, octaédriques, semi-octaédriques ou prismatiques trigonaux.

7. Structures des métaux et alliages

Les métaux se distinguent des autres types de solides par bon nombre de leurs propriétés physiques, dues à leur type de liaison : la liaison métallique.

Bien que les trois quarts des éléments chimiques soient métalliques, seuls quelques-uns se rencontrent à l’état natif: Cu, Ag, Au, Fe, Ni, Hg, les métaux de la mine du platine, et, exceptionnellement, Zn, Sn, Pb, In et Cd, ainsi qu’un grand nombre d’alliages et de composés intermétalliques.

Aussi bien la théorie la plus simple concernant l’état métallique que la théorie de Bloch (cf. physique des SOLIDES), décrivent une liaison non dirigée ainsi qu’un empilement compact pour la plupart des métaux vrais et des métaux de transition. En plus des empilements cubiques et hexagonaux compacts, l’empilement cubique centré, légèrement moins comptact, ayant un atome métallique à chaque sommet du cube, ainsi qu’au centre, est aussi important, spécialement pour les métaux de transition.

Les structures des alliages dépendent fortement des particularités de leurs constituants: ceux-ci peuvent être des métaux vrais ou des métaux de transition du groupe A (éléments à faible électronégativité) du système périodique, plus des métaux, métalloïdes et des non-métaux du groupe B (à forte électronégativité). Les principales combinaisons intéressantes sont A-A, A-B (métal), A (métal de transition)-B (élément non métallique léger: alliage interstitiel, comme par exemple le carbone C dans 塚-Fe) et B-B (métaux). Les structures des alliages sont donc définies par la combinaison de: facteurs géométriques (rayons métalliques des atomes, contraintes sur la coordinence); différences d’électronégativité entre atomes; rôles respectifs des liaisons chimiques dirigées et non dirigées; configuration de la bande d’énergie. Tous ces facteurs subissant l’influence de la pression et de la température.

Avec de faibles différences entre rayons atomiques, des solutions solides étendues, entre métaux A-A, existent, ordonnées ou désordonnées ^{[cf. ALLIAGES]}. Avec de plus grandes différences entre rayons atomiques, on obtient une série de structures intermédiaires, déterminées par les rapports des rayons des atomes constituants, les structures d’alliages par empilement , comme par exemple les phases de Laves dont le type est la structure MgCu² (fig. 3) pour laquelle le rapport idéal des rayons est 連3 / 連2. L’accroissement de la différence entre les électronégativités mène à des liaisons fortes et dirigées et, ainsi, à des composés intermétalliques nombreux pour les catégories A-B (métal) et B-B. Dans les séries d’alliage de même type, entre lesquelles les coordinences ne varient pas de façon significative, les faibles différences d’énergie, liées aux remplissages des zones de Brillouin deviennent importantes: elles limitent la miscibilité de ce que l’on nomme phases électroniques ou phase de Hume-Rothery , (par exemple dans les laitons Cu-Zn) et contrôlent les dimensions des domaines antiphases et autres phénomènes périodiques à longue distance dans quantités d’alliages (par exemple CuAuII, cf. MÉTALLURGIE).

8. Cas des cristaux moléculaires

Les types de forces les plus faibles dans les cristaux sont les faibles forces attractives, dites de Van der Waals, qui lient ensemble des atomes aux valences saturées et des molécules, dans les cristaux moléculaires. Elles existent dans tous les systèmes de cristaux mais sont négligeables dans toutes les structures possédant un système de liaisons plus fortes, tridimensionnel, de quelque type que ce soit. Les forces de Van der Waals ne sont pas dirigées et l’arrangement structural des molécules est déterminé par des considérations purement géométriques (empilement compact).

Plus le nuage électronique est étendu, plus les molécules sont polarisables, donnant des forces de Van der Waals plus grandes pour les éléments les plus lourds de chaque groupe du système périodique. Simultanément, un accroissement des recouvrements orbitaux conduit à une liaison partiellement métallique ou covalente (par exemple, dans la séquence ², Cl², Br², I²).

Rares sont les substances naturelles qui forment des cristaux moléculaires même si sont inclus des cas intermédiaires: par exemple, gaz rares, O², ², C², CO, variétés allotropiques de soufre à molécules cycliques (S⁸ dans les formes communes), As⁴S⁴, HgCl², As⁴⁶. Les cristaux moléculaires sont la forme la plus fréquente de beaucoup de substances organiques telles que les hydrocarbures. Quelques substances (comme CH⁴, CO, HCl) présentent des transitions de phases, au-dessus desquelles les molécules peuvent tourner librement, tout en restant à l’état solide. Rares également sont les structures dans lesquelles les «molécules» saturées s’organisent en chaînes , ou rubans parallèles et infinis, par exemple S 秊, Se, Te (caractère métallique croissant), SiS², Si² fibreux, PdCl², et CuCl². Dans les structures feuilletées dont les couches sont à valences saturées, celles-ci sont liées par des forces de Van der Waals; cette configuration est plus fréquente. Habituellement, les couches ont à leur surface des anions fortement polarisables. Des exemples importants sont fournis par les halogénures de cadmium (CdI², CdCl²) et des sulfures (FeS et MoS²), (tabl. 2), comme par HgI², As²S³ (orpiment) et des silicates en feuillets tels que le talc, Mg³ (Si⁴¹⁰) (OH)².

Les rayons de Van der Waals décrivent les distances entre atomes non liés entre eux par une liaison forte. Si deux atomes, dans une structure ou dans une molécule, sont liés à un troisième atome commun, ils auront tendance à se rapprocher jusqu’à la limite permise par leur interaction non liante (dans la partie à forte pente du potentiel d’interaction). Les forces de Van der Waals correspondent à un bilan entre forces attractives et répulsives, avec des énergies d’interaction de l’ordre de 1 kilojoule par mole, tandis que les contacts non liants à l’intérieur de la molécule mettent en jeu des énergies d’interaction de l’ordre de 10 à 20 kilojoules par mole. À titre de comparaison, la formation de liaisons chimiques met en jeu des énergies de l’ordre de plusieurs centaines de kilojoules par mole. Les contacts non liants régissent les limites de déformation dans les structures flexibles (telles que la cristobalite et la tridymite, de même formule, Si²), la configuration des petites molécules ainsi que les variations des longueurs de liaisons dues à des contraintes stériques.

9. Tendances de la cristallochimie

Principe de construction des structures

Beaucoup de structures à grande échelle peuvent être décrites comme des zones structuralement uniformes, d’un certain type qui est modifié par intervalles (habituellement réguliers) par des zones à coordinence et composition altérées. Les principes selon lesquels sont bâties ces zones modifiées représentent les types de défauts structuraux à grande échelle ou, dans le cas de répétitions suffisamment fréquentes et régulières, les opérateurs de construction des structures par le biais desquels une nouvelle structure s’élabore, issue d’une structure parentale plus simple. Ainsi les plans de cisaillement cristallographique représentent les plans réticulaires (h , k , l ) régulièrement espacés, sur lesquels un vecteur de déplacement [u , v , w ], non parallèle au plan, décrit les connexions locales des blocs structuraux ayant la même orientation. Ces connexions se réalisent par des défauts anioniques, par exemple dans des oxydes tels que Ti^2– size=1^嗀 ou dans le système [W³(Ta, Nb)²⁵].

Le maclage chimique (ou maclage de maille)

Le maclage chimique (ou maclage de maille) représente un maclage sur des miroirs ou des plans de glissement (rarement un maclage cyclique) d’arrangements atomiques relativement simples. Les plans de composition contiennent des cations dont les coordinences diffèrent de celles du reste de la structure (souvent prismatiques trigonales). Fe³C, Y³, CaUS³, Cu³SbS³, LnFe³ et U²FeS⁵ représentent des exemples d’empilements compacts hexagonaux, ainsi maclés selon (11 露2), ayant des lamelles de structure hexagonale compacte d’épaisseurs différentes entre les plans de composition adjacents. UFeS³, BaCu⁴S³, CaTi²⁴, Pb³Bi²S⁶ sont des exemples d’arrangements cubiques compacts maclés selon (113). Les portions reliées par le miroir peuvent être de même épaisseur ou d’une épaisseur différente. Si les opérateurs de construction des structures agissent sur l’arrangement atomique de base avec des fréquences différentes, des séries homologues de composés sont engendrées, qui ne diffèrent que par l’épaisseur des lamelles et les variations de proportions des éléments chimiques correspondantes.

Alors que le maclage cristallographique est un état dans lequel les «erreurs» (plans de composition) élèvent le niveau d’énergie interne au-dessus de celui du composé non maclé, l’énergie interne du composé maclé chimiquement est inférieure à celle d’un composé non maclé ayant une «structure de base» de même composition. Les frontières des domaines antiphases déplacent périodiquement des portions adjacentes de la structure, le plus souvent de la moitié du module d’un des vecteurs de base du réseau, situé dans leur plan (par exemple, dans Nb²Zr⁶¹⁷ ou dans CuAuII). Finalement, il peut exister une incommensurabilité géométrique entre deux ensembles de couches alternées (ou ensembles de fragments de couches, composés à couches tels que FePb³Sn⁴Sb²S¹⁴ ou FeCuS² . 1,53 [Mg⁰,⁶⁷Al⁰,³³(OH)²]) ou entre la matrice et les colonnes d’espèces atomiques distinctes (par exemple Ba¹⁰(FeS²)¹⁸ ou Mn¹⁵Si²⁶). Chacun des ensembles a sa propre périodicité, ces deux périodicités ne sont commensurables qu’au bout d’un grand nombre de mailles élémentaires. La non-conformité peut éventuellement être éliminée par des domaines antiphases, des cisaillements cristallographiques ou autres opérateurs.

Ces nouveaux concepts de la cristallochimie sont en plein développement.

Encyclopédie Universelle. 2012.